Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách tính diện tích tam giác được tạo bởi ba điểm cực trị của hàm số.
Thông thường, đề bài chỉ cho bạn hàm số rồi yêu cầu bạn tính diện tích tam giác, vậy nên công việc đầu tiên bạn cần làm là tìm ra ba điểm cực trị.
Khi tìm được ba điểm cực trị rồi thì đồng nghĩa với việc bạn đã đi được một phần hai đoạn đường, phần còn lại bạn chỉ việc áp dụng một trong các cách bên dưới là xong.
Okay, ngay bây giờ chúng ta sẽ vào phần nội dung chính ngay nhé !
Mục Lục Nội Dung
Cách #1. Dựa vào định thức của ma trận vuông cấp 2 x 2
Cách này sử dụng kiến thức của Đại số cao cấp, chủ yếu là kiến thức của Đại số tuyến tính.
Bước 1. Tìm ba điểm cực trị của đồ thị hàm số f(x)
Giả sử chúng ta tìm được $A=(x_a; y_a), B=(x_b; y_b), C=(x_c; y_c)$ là ba điểm cực trị của đồ thị hàm số đã cho.
Bước 2. Tính véc tơ $\overrightarrow{AB}=(x_b-x_a; y_b-y_a), \overrightarrow{AC}=(x_c-x_a; y_c-y_a)$
Để thuận tiện cho việc trình bày, ở đây mình sẽ đặt $\overrightarrow{AB}=(a; b), \overrightarrow{AC}=(c; d)$
Bước 3. Tính giá trị biểu thức $\left|\begin{array}{cc}a&b\\c&d\end{array}\right|=ad-cb$
Bước 4. Giá trị của biểu thức $\frac{|ad-cb|}{2}$ chính là diện tích tam giác ABC
Ví dụ 1. Tính diện tích tam giác tạo bởi ba điểm cực trị của đồ thị hàm số $f(x)=3x^4-40x^3+186x^2-360x$

Lời giải:
Dễ thấy, ba điểm cực trị của đồ thị hàm số $f(x)=3x^4-40x^3+186x^2-360x$ là lượt là $A=(2; -248), B=(3; -243), C=(5; -275)$
Véc tơ $\overrightarrow{AB}, \overrightarrow{AC}$ lần lượt là $(1; 5), (3; -27)$
$\left|\begin{array}{cc}1&5\\3&-27\end{array}\right|=1(-27)-5.3=-42$
$S_{ABC}=\frac{|-42|}{2}=21$
Vậy diện tích tam giác ABC là 21 ĐVDT
Cách #2. Sử dụng công thức Hê-rông
Ở cách này chúng ta sẽ chuyển từ bài toán Giải tích cổ điển sang bài Hình học sơ cấp nhờ vào công thức tính khoảng cách giữa hai điểm.
Giả sử điểm $A=(x_a; y_a), B=(x_b; y_b)$ lúc bấy khoảng cách giữa hai điểm A, B sẽ được tính theo công thức $\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}$
2.1. Về các bước giải như sau:
Bước 1. Tính độ dài các cạnh AB, BC, CA
Bước 2. Áp dụng công thức Hê rông
Để thuận tiện cho việc trình bày, ở đây mình sẽ đặt $AB=a, BC=b, CA=c, p=\frac{a+b+c}{2}$
Lúc bấy giờ diện tích của tam giác ABC sẽ được tính theo công thức $\sqrt{p(p-a)(p-b)(p-c)}$
Ví dụ 2. Tính diện tích tam giác tạo bởi ba điểm cực trị của đồ thị hàm số $f(x)=3x^4-40x^3+186x^2-360x$
Lời giải:
Dễ thấy ba điểm cực trị của đồ thị hàm số $f(x)=3x^4-40x^3+186x^2-360x$ là lượt là $A=(2; -248), B=(3; -243), C=(5; -275)$
Độ dài ba cạnh AB, BC, CA lần lượt là $\sqrt{26}, 2\sqrt{257}, 3\sqrt{82}$
Nửa chu vi $\frac{\sqrt{26}+2\sqrt{257}+3\sqrt{82}}{2}$
Vậy diện tích tam giác ABC là 21 ĐVDT
2.2. Thu gọn biểu thức phức tạp bằng máy tính CASIO
Như các bạn có thể thấy, biểu thức trên khá là phức tạp, không nói tới việc bạn thu gọn “bằng tay”, cho dù bạn thu gọn bằng máy tính CASIO bằng cách nhập trực tiếp biểu thức thì vẫn tốn khá nhiều thời gian và dễ bị sai sót
Giải pháp là bạn hãy gán $\sqrt{26}, 2\sqrt{257}, 3\sqrt{82}, \frac{\sqrt{26}+2\sqrt{257}+3\sqrt{82}}{2}$ lần lượt vào các biến nhớ A, B, C, D rồi tính giá trị biểu thức $\sqrt{D(D-A)(D-B)(D-C)}$
Cách gán giá trị vào biến nhớ như sau:
Nhập giá trị => nhấn phím STO => nhấn phím biến nhớ.
Cụ thể như sau:
Lần lượt nhấn các phím …
Các bước thực hiện:
Bước 1. Gán các giá trị vào các biến nhớ.

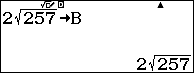
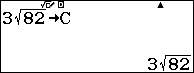

Bước 2. Nhập biểu thức:
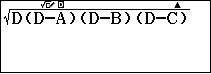
Bước 3. Nhấn phím =
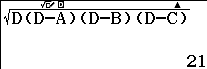
Cách #3. Sử dụng công thức đặc biệt
Cách 1 và Cách 2 có thể áp dụng với mọi hàm số, miễn sao hàm số có ba điểm cực trị không thẳng hàng là được.
Còn riêng cách số 3 này chỉ áp dụng được với hàm số $f(x)=ax^4+bx^2+c$ với điều kiện a và b trái dấu các bạn nhé.
Lúc bấy giờ, diện tích tam giác tạo bởi ba điểm cực trị của đồ thị hàm số $f(x)=ax^4+bx^2+c$ sẽ được tính theo công thức $\sqrt{-\frac{b^5}{32a^3}}$
Ví dụ 3. Tính diện tích tam giác tạo bởi ba điểm cực trị của đồ thị hàm số $f(x)=3x^4-7x^2$
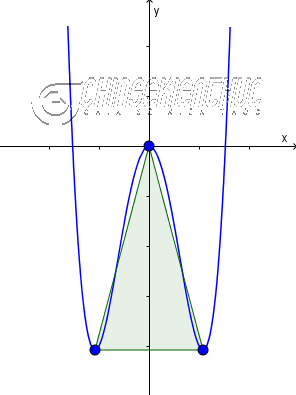
Lời giải:
Diện tích tam giác tạo bởi ba điểm cực trị của đồ thị hàm số $f(x)=3x^4-7x^2$ sẽ bằng $\sqrt{-\frac{(-7)^5}{32.(3)^3}}=\frac{49\sqrt{42}}{72}$
Vậy diện tích tam giác cần tìm là $\frac{49\sqrt{42}}{72} \approx 4.41$ ĐVDT
#4. Lời kết
Okay, trên đây là 3 cách tính diện tích tam giác tạo bởi ba điểm cực trị mà mình muốn chia sẻ với bạn trong bài viết này. Trong hầu hết các trường hợp bạn nên ưu tiên sử dụng Cách 1 để giải bài tập nhé.
Cách 3 tuy rất nhanh nhưng khả năng ứng dụng khá hạn chế, chỉ khi nào hàm số đã cho là hàm trùng phương, a và b trái dấu thì mới có thể áp dụng được.
Ngoài ra, để tính được diện tích tam giác được tạo ra bởi ba điểm cực trị bạn cũng nên xem lại cách tính tích có hướng, công thức tính diện tích tam giác…
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Note: Bài viết này hữu ích với bạn chứ? Đừng quên đánh giá bài viết, like và chia sẻ cho bạn bè và người thân của bạn nhé !
Xem Them Chi Tiet
Nhung Mon Do Cong Nghe Duoc Yeu Thich
Do Cong Nghe Phu Kien


Không có nhận xét nào:
Đăng nhận xét